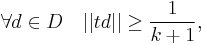Lonely runner conjecture
In number theory, and especially the study of diophantine approximation, the lonely runner conjecture is a conjecture originally due to J. M. Wills in 1967. Applications of the conjecture are widespread in mathematics; they include view obstruction problems[1] and calculating the chromatic number of distance graphs and circulant graphs.[2] The conjecture was given its picturesque name by L. Goddyn in 1998.[3]
Contents |
The conjecture
Consider k + 1 runners on a circular track of unit length. At t = 0, all runners are at the same position and start to run; the runners' speeds are pairwise distinct. A runner is said to be lonely if at distance of at least 1/(k + 1) from each other runner. The lonely runner conjecture states that every runner gets lonely at some time.
A convenient reformulation of the problem is to assume that the runners have integer speeds, not all divisible by the same prime; the runner to be lonely has zero speed. The conjecture then states that for any set D of k positive integers with gcd 1, there exists a real t such that
where ||x|| denotes the distance of real number x to the nearest integer.
Known results
| k | year proved | proved by |
|---|---|---|
| 3 | 1972 | Betke and Wills[4]; Cusick[5] |
| 4 | 1984 | Cusick and Pomerance[6]; Bienia et al.[3] |
| 5 | 2001 | Bohman, Holzman, Kleitman[7]; Renault[8] |
| 6 | 2008 | Barajas and Serra[2] |
Notes
- ^ T. W. Cusick (1973). "View-Obstruction problems". Aequationes Math. 9 (2–3): 165–170. doi:10.1007/BF01832623.
- ^ a b J. Barajas and O. Serra (2008). "The lonely runner with seven runners". The Electronic Journal of Combinatorics 15: R48.
- ^ a b W. Bienia et al. (1998). "Flows, view obstructions, and the lonely runner problem". Journal of combinatorial theory series B 72: 1–9. doi:10.1006/jctb.1997.1770.
- ^ Betke, U.; Wills, J. M. (1972). "Untere Schranken für zwei diophantische Approximations-Funktionen". Monatshefte für Mathematik 76 (3): 214. doi:10.1007/BF01322924.
- ^ T. W. Cusick (1974). "View-obstruction problems in n-dimensional geometry". Journal of Combinatorial Theory, Series A 16 (1): 1–11. doi:10.1016/0097-3165(74)90066-1.
- ^ Cusick, T.W.; Pomerance, Carl (1984). "View-obstruction problems, III". Journal of Number Theory 19 (2): 131–139. doi:10.1016/0022-314X(84)90097-0.
- ^ Bohman, T.; Holzman, R.; Kleitman, D. (2001), "Six lonely runners", Electronic Journal of Combinatorics 8 (2)
- ^ Renault, J. (2004). "View-obstruction: A shorter proof for 6 lonely runners". Discrete Mathematics 287: 93–33. doi:10.1016/j.disc.2004.06.008.